Física

 
Tabela de conteúdos

1. Definição e classificação de sistemas
2. Transferência de energia entre sistemas
  2.1. Rendimento das transferências energéticas
  2.2. Transferência de energia por calor
  2.3. Transferência de energia por trabalho
    . 2.3.1. Gráficos posição-tempo e velocidade-tempo em movimentos rectilíneos
  2.4. Transferência de energia por radiação
    . 2.4.1. A temperatura média da Terra
Actividade laboratoriais
  AL 10.0.1. Rendimento no aquecimento
  AL 10.1.1. Absorção e emissão de radiação
  AL 10.1.2. Energia eléctrica fornecida por um painel fotovoltaico
  AL 10.1.3. Capacidade térmica mássica
  AL 10.1.4. Balança energético num sistema termodinâmico
  AL 10.2.1. Energia cinética ao longo de um plano inclinado
  AL 10.2.2. Coeficiente de restituição
  AL 11.1.0. Movimentos unidimensionais
  AL 11.1.1. Queda livre
  AL 11.1.2. Movimento de um corpo com e sem força resultante nula
  AL 11.1.3. Lançamento horizontal sem forças dissipativas
  AL 11.2.1. Osciloscópio
  AL 11.2.2. Velocidade do som no ar

1. Definição e classificação de sistemas

   Um sistema pode ser qualquer porção do Universo constituída por massa e energia que queiramos avaliar e investigar separadamente. Em relação ao meio envolvente, os sistemas podem ser: isolados, quando não se dão trocas nem de energia nem de massa com o meio exterior; fechados, quando não há trocas de massa com o meio, mas a energia pode entrar e sair do sistema; ou abertos, quando há transferência de massa e de energia com o meio.

   Mas os sistemas estudados pela Física também podem ser classificados como termodinâmicos, mecânicos ou complexos.

• Termodinâmicos são aqueles em que, visto as partículas que o constituem se encontrarem em movimento relativo constante, não se desprezam as variações de energia cinética, mas apenas as de energia mecânica (exemplo: panela ao lume); 
• Mecânicos são aqueles em que as variações de energia interna (e, consequentemente, temperatura) são desprezáveis, analisando-se, somente, as variações de energia mecânica (exemplo: bola a rolar ao longo de uma encosta); 
• Complexos são, simultaneamente, termodinâmicos e mecânicos, já que não se desprezam nem as variações de energia cinética nem as de energia mecânica (exemplo: automóvel).

2. Tranferência de energia entre sistemas

 2.1. Rendimento das transferências energéticas

   Nas transferências de energia de um sistema para outro, há sempre uma porção de energia utilizada para o fim desejado (energia útil) e uma porção de energia que se dissipa, isto é, não é aproveitada para tal, degradando-se (= perdendo qualidade)ⁱ. Segundo a Lei da Conservação da Energiaⁱⁱ, a soma da energia útil com a dissipada será igual ao valor da energia fornecida.

   O rendimento de um processo destina-se a indicar a quantidade de energia aproveitada para o fim pretendido por cada 100 unidades de energia fornecida.

$$E_{dissipada}=E_{fornecida}-E_{\acute{u}til}$$
$$\eta = \frac{P_{\acute{u}til}}{P_{fornecida}} \times 100 \% = \frac{\frac{E_{\acute{u}til}}{\Delta t}}{\frac{E_{fornecida}}{\Delta t}} \times 100 \% = \frac{E_{\acute{u}til}}{E_{fornecida}} \times 100 \% $$

 2.2. Tranferência de energia por calor

   A temperatura de um corpo (T, quando expressa em K, e θ, quando expressa em ºC) traduz a energia cinética média de agitação das suas partículas. Não deve ser confundido com a energia térmica de um corpo (expressa em joules, J), que é a energia cinética total de agitação das suas partículas. Daqui se conclui que dois corpos do mesmo material com a mesma temperatura poderão ter valores de energia térmica diferentes se a sua massa for diferente, já isto implica um número de partículas diferente e, por extensão, um valor de energia cinética total de agitação diferente.

   A energia interna (E_i) de um corpo (expressa em joules, J) é a soma da energia cinética total de agitação das suas partículas com a energia potencial de interacção entre elas. Deste modo, dois corpos do mesmo material com a mesma temperatura poderão ter valores de energia interna diferentes se a sua massa for diferente, já que isto implica um número de partículas diferente e, por extensão, um valor diferente de energia potencial de interacção entre as partículas.

   A variação de energia interna de um sistema é igual ao balanço da energia por ele recebida e por ele cedida na forma de trabalho (W), calor (Q) e radiação (R)ⁱⁱⁱ, o que é traduzido pela 1ª Lei da Termodinâmica.

   Quando a temperatura de dois corpos em contacto entre si é diferente, dão-se transferências de energia em que o corpo com maior temperatura cede mais energia do que recebe e o com menor temperatura recebe mais energia do que cede até que se atinja o equilíbrio térmico^iv. A esta energia transferida dá-se o nome de calor (Q, que é expresso em joules, J), podendo a troca processar-se de dois modos diferentes: condução ou convecção.
   A condução consiste na transferência de energia através das colisões entre partículas, sendo que aquelas com maior energia cinética cedem energia às de menor energia. Durante este processo, não há deslocamento de matéria, mas apenas das suas partículas (ou seja, não há movimento macroscópico, mas sim microscópico). Para avaliar a capacidade que uma substância tem de receber ou transmitir energia deste modo, utilizamos a sua condutividade térmica (k, expresso em W m^-1 K^-1), que se define como a quantidade de calor (Q, que é expresso em joules, J) que atravessa, por segundo (Δt), a espessura (L) de 1 metro entre duas superfícies paralelas de área (A) igual a 1 m², quando a diferença de temperaturas (ΔT) entre estas é 1 K.

   A fórmula para o cálculo do calor a partir da condutividade térmica pode ser utilizada para encontrar a temperatura de dois corpos em contacto um com o outro (estando os pontos a temperaturas diferentes a uma distância L um do outro), constituindo um sistema isolado (pelo que a energia cedida por um será igual à recebida pelo outro), quando estes atingem o equilíbrio térmico (a sua temperatura final será igual).

   Analisando uma tabela dos valores de condutividade térmica de algumas substâncias, verificamos que os sólidos e, em particular, os metais são bons condutores. Tal sucede porque as partículas de que uma substância é formada (átomos, moléculas, iões...) estão, regra geral, mais próximas umas das outras quando o material se encontra no estado sólido (química elementar), facilitando-se, deste modo, o contacto e a transferência de energia entre elas. O caso dos metais pode ser explicado devido à ligação metálica que une as suas unidades estruturais, visto que esta pressupõe a existência de electrões livres que possuem maior liberdade de movimentos e, como tal, podem adquirir e transmitir maiores quantidades de energia cinética.
   Os piores condutores (e, por conseguinte, melhores isoladores térmicos) são os líquidos e os gases, nos quais a transferência de calor por condução é muito lenta (o que se deve à sua rarefacção, ou seja, ao facto de as suas unidades estruturais estarem muito afastadas). Assim, as trocas de energia entre substâncias nestes estados físicos dão-se, principalmente, por convecção. Durante este processo, há deslocamento de massas, podendo este ser: natural (convecção natural), quando acontece devido à diferença de densidades (a parte do fluido^v em contacto com uma fonte térmica aquece, torna-se menos denso (visto o seu volume aumentar) e sobe, obrigando a porção mais fria do material a descer), ou forçado (convecção forçada), quando se deve a uma ventoinha ou bomba. Em ambos os casos, os movimentos macroscópicos do fluido levam à uniformização da sua temperatura (equilíbrio térmico).
   Ambos os processos, condução e convecção, são utilizados pelos colectores solares^vi.

   A quantidade de calor recebido por um corpo também pode ser calculada a partir da fórmula que traduz a capacidade térmica mássica de uma substância (c, expresso em J kg^-1 ºC^-1), que corresponde ao valor de energia que é necessário fornecer a 1 kg dessa substância para que a sua temperatura se eleve 1 ºC quando não há mudanças de estado físico envolvidas. Não se deve confundir com a capacidade térmica (C, expresso em J ºC^-1), que estabelece o valor de energia que é necessário fornecer a um corpo para que a sua massa se eleve 1 ºC quando não há mudanças de estado físico envolvidas.

   A fórmula para o cálculo do calor a partir da capacidade térmica mássica pode ser utilizada para encontrar a temperatura de dois corpos em contacto um com o outro, constituindo um sistema isolado (pelo que a energia cedida por um será igual à recebida pelo outro), quando estes atingem o equilíbrio térmico (a sua temperatura final será igual).

   Enquanto um corpo está a sofrer uma mudança de estado físico, recebe energia sem, contudo, variar a sua temperatura. Assim, nestas situações, não podemos aplicar a fórmula da capacidade térmica mássica para calcular o calor por ele absorvido, pelo que utilizamos a variação de entalpia^vii (ΔH, expresso em J kg^-1), ou seja, o valor de energia (Q, expresso em J) que é necessário fornecer a 1 kg dessa substância para que ocorra a mudança.

   A variação de entalpia é positiva quando é necessário fornecer energia ao corpo para que se dê a transição de estado físico (é preciso "aquecê-lo", como na fusão, sublimação (passagem do estado sólido ao gasoso) ou evaporação) e negativa quanto é preciso retirar-lha (é preciso "arrefecê-lo", como na condensação, sublimação inversa (passagem do estado gasoso ao sólido) ou solidificação).

 2.3. Transferência de energia por trabalho

   Quando um corpo sofre uma deformação ou um deslocamento, diz-se que actuou, sobre ele, uma força, tendo este recebido ou cedido energia na forma de trabalho (W, que é expresso em joules, J).

   No caso das deformações, o trabalho das forças que actuam sobre um corpo é potente ou positivo se este é comprimido e resistente ou negativo se o seu volume aumenta. É nulo quando não há variação do seu volume (logo, não há deformação).

   Sobre um corpo indeformável só pode ser realizado trabalho se este for deslocado. Debruçar-nos-emos, agora, sobre este tipo de corpos, que podem ser representados apenas pelo seu centro de massa, um ponto que corresponde, em corpos de constituição uniforme, ao seu centro geométrico. Todas as forças que actuam sobre um corpo são representadas com vectores cuja origem coincide com o centro de massa do mesmo, com excepção da força de atrito que, visto surgir do contacto entre o corpo e a superfície, é representada com um vector de origem no centro do fundo do corpo.

    Para que um corpo fique assente sobre uma superfície plana sem deslocar-se verticalmente (para cima ou para baixo), as forças verticais que actuam sobre ele têm que se anular. Assim, na situação 1, a reacção normal terá a mesma intensidade que a força gravítica e, na situação 2, terá a mesma intensidade que a subtracção de F_y a F_g.

   Uma força aplicada sobre um corpo resulta da adição de duas forças (ver igualdade no final da figura da situação 2): uma paralela ao deslocamento sofrido e outra perpendicular a este. Só a primeira é eficaz para o movimento do corpo, pelo que só esta lhe cede ou retira energia. Assim, o trabalho de uma força sobre um corpo é dada pelo produto da intensidade da sua componente eficaz (primeira expressão, deduzida a partir da figura 6 da página 104 do manual) pelo deslocamento verificado.

   Uma força com o mesmo sentido que o movimento de um corpo exerce sobre ele um potente ou positivo (porque α será um ângulo agudo, ou seja, inferior a 90º, pelo que cos α > 0) e, se tiver sentido oposto, exercerá um trabalho resistente ou negativo (porque α será um ângulo obtuso, ou seja, superior a 90º, pelo que cos α < 0). O trabalho de uma força é nulo quando esta é perpendicular ao deslocamento (porque α será um ângulo recto, ou seja, igual a 90º, pelo que cos α = 0).
   Voltando às situações 1 e 2, a força resultante que actua sobre o corpo é a soma de todas as forças aplicadas sobre ele^viii, pelo que o seu trabalho será igual à soma da energia que estas fornecem ao corpo por trabalho. De acordo com a Lei do Trabalho-Energia^ix, visto que o trabalho da força resultante que actua sobre um corpo indeformável se traduzirá no movimento do mesmo, este corresponderá à sua variação de energia cinética (a energia associada ao movimento).

   Então, quando o trabalho da força resultante é potente ou positivo, o corpo ganhará velocidade, ganhando energia cinética (já que a velocidade final será superior à inicial). Se porém, o vector da força resultante contrariar o movimento pretendido, verificar-se-á uma redução da velocidade e, consequentemente, da energia cinética do corpo (porque a velocidade final será inferior à inicial).
   Centremo-nos, agora, no trabalho realizado pela força gravítica. Aplicando a fórmula para o cálculo do trabalho de uma força, temos trabalho positivo durante a descida (já que a força gravítica contribui para este movimento, fazendo um ângulo de 0º com ele, e que cos 0º = 1) e negativo durante a subida (já que a força gravítica contraria este deslocamento, fazendo um ângulo de 180º com ele, e que cos 180º = -1). O deslocamento será dado pela distância percorrida pelo corpo que, como se dá na vertical, corresponde a um valor de altura. Por fim, a intensidade, de acordo com a 2ª Lei de Newton^x, traduz-se pelo produto da massa do corpo pela aceleração por ele adquirida, que é, neste caso, a aceleração gravítica, g^xi. Em suma:

   Podemos, porém, simplificar estes cálculos deduzindo o trabalho da força gravítica a partir da energia potencial gravítica, que é a energia resultante da interacção com a Terra que os corpos possuem armazenada e pronta a manifestar-se. Esta é directamente proporcional à força gravítica^ix (quanto maior a sua intensidade, maior a energia potencial gravítica de um corpo) e à altitude (à medida que aumenta a altitude de um corpo, cresce a distância que o separa da Terra, aumentando a sua energia potencial gravítica). Ou seja:

    Este tipo de igualdade pode ser aplicada a todas as forças conservativas, mas, no caso das forças elástica e eléctrica, por exemplo, as energias correspondentes são a potencial elástica e a potencial eléctrica, respectivamente. Tal sucede porque o trabalho destas forças quando causam o deslocamento de um corpo dependem apenas da posição final e inicial do mesmo, independentemente da trajectória.

   Assim, num percurso fechado, em que a posição final e inicial são iguais, o trabalho de uma força conservativa será nulo, já que a energia potencial final será igual à energia potencial inicial (a variação de energia potencial será zero).
   Mas o que são forças conservativas? São forças que, ao actuarem sozinhas sobre um sistema, não alteram a sua energia mecânica, obedecendo à Lei da Conservação da Energia Mecânica^xii.
   Durante a descida, a distância entre este a Terra decresce e, consequentemente, diminui a sua energia potencial gravítica. Visto que o corpo adquire velocidade durante a queda, considerando que a única força a actuar sobre um corpo é a gravítica (não há atrito nem quaisquer outras forças), a energia potencial gravítica converte-se em energia cinética, ou seja, estas serão simétricas uma da outra.

   Há, portanto, uma variação de energia mecânica (= soma da energia cinética com as energias potenciais de um corpo) nula, pelo que há conservação desta. Assim, a força gravítica, de acordo com a Lei da Conservação da Energia Mecânica, é conservativa.
   Quando actuam sobre um corpo tanto forças conservativas como não conservativas, a sua variação de energia mecânica é dada pelo trabalho das não conservativas.

   2.3.1. Gráficos posição-tempo e velocidade-tempo em movimentos rectilíneos

   Quando a posição de um corpo (grandeza física de carácter vectorial (isto é, é caracterizada por direcção, sentido, intensidade e ponto de aplicação) representada por um vector que une a origem do referencial ao ponto (= corpo) em estudo) relativamente^xiii a um referencial^xiv se altera ao longo do tempo, dizemos que este está em movimento (caso contrário, está em repouso). À união das posições sucessivas que um corpo ocupa dá-se o nome de trajectória, que pode ser rectilínea ou curvilínea.

   Mas, para caracterizarmos um movimento, não basta identificar a sua trajectória e o sentido segundo o qual o corpo se desloca. Podemos utilizar três outros parâmetros: rapidez média (grandeza física escalar positiva que mede o espaço percorrido sobre a trajectória, s, por unidade de tempo e é expressa em m/s), ou r_m, velocidade média^xv e aceleração média.

   O modo como a posição de um corpo evolui ao longo do tempo pode ser descrito por um uma função x = x(t), em que t é o instante e x é a posição que lhe corresponde. Esta pode ser representada por um gráfico posição-tempo que permitirá caracterizar o sentido do movimento: quando x = x(t) é crescente, o corpo em estudo desloca-se no sentido positivo da trajectória; quando é descrescente, o deslocamento faz-se segundo o sentido negativo; e, quando é constante, o corpo está em repouso (visto que não há alteração da sua posição relativamente ao referencial). Os zeros da função x = x(t) representam passagens do corpo pela origem do referencial e os mínimos e máximos pontos em que este inverte o sentido da trajectória.

   Embora tenham pontos comuns, é fácil  verificar que os gráficos 1 e 2 são diferentes: o primeiro é composto, somente por linhas rectas, enquanto o segundo apresenta várias linhas curvas e uma linha recta no intervalo de tempo [10, 15]. Nos intervalos de tempo para os quais a função x = x(t) é uma recta, a velocidade é constante, visto que a velocidade média escalar é igual ao declive, m, da recta.

   Quando x = x(t) não é uma recta, a velocidade média escalar num instante é dada pelo declive da recta tangente à curva. Por exemplo, no intervalo de tempo [0, 10] do gráfico 2, o declive das rectas tangentes^xvi é cada vez menor, o que nos leva a concluir que a velocidade também está a reduzir-se.

   Do mesmo modo que desenhamos x = x(t), podemos esboçar um gráfico velocidade-tempo, a representação  da função v = v(t), como o gráfico 3:

   Num gráfico velocidade-tempo, o deslocamento (= variação de posição) do corpo em estudo num intervalo de tempo será igual à área que lhe corresponde. Utilizemos como exemplo o intervalo [30; 45] do gráfico 3:

   Nos intervalos de tempo para os quais a função v = v(t) é uma recta, a aceleração é constante, visto que a aceleração média escalar é igual ao declive, m, da recta.

 2.4. Transferência de energia por radiação

   De acordo com a Lei da Conservação da Energia, o total de energia transportada pela radiação que incide num corpo 1 é igual à soma das fracções desta energia que ele absorve (α), reflecte (ρ) e transmite (= refracta, ι): 1 = α + ρ + ι. Quando um corpo é opaco a um dado tipo de radiação, não a transmite (ι = 0), pelo que só a absorve ou reflecte (α + ρ = 1). Por outro lado, α, ρ e ι dependem da frequência da radiação, porque os corpos podem emitir, reflectir ou transmitir de forma diferente diferentes frequências de radiação electromagnética.

   Todos os corpos a uma temperatura superior a 0 K emitem radiação electromagnética. Quanto maior a temperatura do corpo, menor o comprimento de onda (porque a frequência aumenta da radiação, numa relação de proporcionalidade inversa.

   A potência total, em todas as frequências, irradiada por um corpo, segundo a Lei de Stephan-Boltzmann, é directamente proporcional à área da superfície so mesmo (A, em m²), à sua emissividade (ε, que, visto ser igual ao seu valor de α, só pode tomar valores entre 0 e 1^xvii) e à quarta potência da sua temperatura (T, em K). Assim, à medida que aumenta a temperatura do corpo, aumenta a intensidade da sua radiação (I, expresso em W m^-2), isto é, a potência emitida por unidade de superfície.

   2.4.1. A temperatura média da Terra

   A Terra está em equilíbrio radiativo (e não térmico, já que este último pressupõe uma igualdade de temperaturas): a energia que esta absorve é igual à energia que emite num mesmo intervalo de tempo, ou seja, a potência recebida e a potência irradiada são iguais.

   Visto que, segundo a Lei da Conservação da Energia, 1 = α + ρ, para corpos opacos, e que ρ = albedo = 0,3 = 30%, podemos afirmar que 70% da energia que incide sobre o planeta é absorvida (α). Considerando que a constante solar, S, é o valor da potência da radiação solar directa^xviii por unidade de área da superfície e que a superfície onde esta incide é um círculo de raio igual ao da Terra, temos:

   Sabendo que o quociente entre a área do círculo que consideramos e a área da superfície da Terra é 1/4, o poder absorsor da Terra será 1/4 da intensidade da radiação solar incidente, ou seja, 1370 / 4 = 343 W m^-2.

   Assim, os 343 W m^-2 são divididos em duas partes: o que é absorvido e, depois, emitido (poder emissor) e o que é reflectido (poder reflector). Sabendo que o albedo da Terra é 30%, sabe-se que 30% dos 343 W m^-2 são reenviados para o espaço (poder reflector), não contribuindo para o aquecimento do planeta. O poder emissor (a intensidade, isto é, a potência irradiada pela Terra por unidade de área), será, então 343 - (343*0,3) = 240 W m^-2. Então, temos:

   O valor da temperatura que se obteve, 255 K, está, no entanto, abaixo do valor real à superfície, 288 K (25ºC). A que se deve o erro?

1. A Terra e o Sol são considerados, nestes cálculos, como corpos negros, ou seja, um corpos com ε = 1, embora a emissividade de cada um destes astros seja inferior à unidade.
2. O valor da constante solar, S, é uma mera aproximação.
3. A esfericidade da Terra foi desprezada, considerando-se como superfície de incidência de luz solar um círculo de raio igual ao da Terra.
4. Não foi tomado em conta o efeito de estufa^xix, que consiste na absorção dos raios IV libertados pela Terra por parte de diversos gases nas camadas baixas da atmosfera com consequente emissão dos mesmos (sendo que parte dessa energia é reenviada para a superfície do planeta).

Actividades laboratoriais

 AL 10.0.1. Rendimento no aquecimento

   Durante a primeira actividade laboratorial, calculámos o rendimento do aquecimento de uma massa de água numa placa para o efeito. Para o fazer, temos que determinar dois valores: a energia fornecida e a energia útil:

• A energia fornecida corresponde ao valor de energia emitido pela placa de aquecimento. Sabendo que P=E/∆t e que, visto esta ser um aparelho eléctrica, a sua potência também pode ser determinada pelo produto da intensidade da corrente pela tensão (P=UI).
• A energia útil é a que é utilizada para causar um aumento de temperatura da água, logo pode ser calculada pela célebre fórmula do calor: Q=mc∆θ.

Assumindo que não se agitou a mistura durante a actividade experimental, como variaria o rendimento do aquecimento se se repetisse o procedimento usando um agitador magnético? O rendimento dependeria da posição do sensor de temperatura: caso este estivesse mergulhado no líquido e próximo da fonte de calor, o rendimento com o agitador magnético seria menor do que sem ele; se este estivesse mergulhado no líquido mas próximo da superfície, verificar-se-ia o contrário.

Assumindo que se utilizou um gobelé (de vidro) na actividade experimental, como variaria o rendimento do aquecimento se se repetisse o procedimento usando um recipiente metálico? Com a substituição do gobelé (recipiente de vidro) por um recipiente de metal, conseguir-se-ia um rendimento superior ao obtido na primeira experiência devido à maior condutividade deste material (que permite a transferência de maior quantidade de energia no intervalo de tempo de aquecimento).

Como variaria o rendimento do aquecimento se se repetisse o procedimento substituindo o recipiente usado por um do mesmo material mas com uma área de base maior? Obter-se-ia um maior valor de rendimento, pois aumentar-se-ia a área de contacto entre a placa e o recipiente, reduzindo-se as dissipações de calor.

De que outras formas poderíamos provocar um aumento no rendimento da actividade experimental? O rendimento do aquecimento seria maior se o procedimento tivesse sido realizado dentro de um calorímetro (reduzem-se as trocas de energia com o meio) e maior ainda se este aparelho não possuísse no seu interior.

 AL 10.1.1. Absorção e emissão de radiação

   Durante a segunda actividade laboratorial, analisámos a emissão e absorção de três latas (uma metalizada, uma pintada de preta e uma pintada de branco) durante o seu aquecimento (foram iluminadas por um candeeiro) e posterior arrefecimento. Através do gráfico obtido pela máquina de calcular, verificaram-se valores semelhantes aos seguintes:

Que transferências de energia ocorreram durante o aquecimento e arrefecimento? Durante o aquecimento, o candeeiro emitiu radiação electromagnética que transferiu energia para o ar (energia dissipada) e para as latas (energia útil). Estas, por sua vez, transferiram energia para o ar no seu interior e para o meio circundante (emitem radiação visto estarem a uma temperatura superior a 0 K).

Durante o arrefecimento, cessa-se a emissão de radiação, pelo que as únicas transferências de energias verificadas ocorrem entre as latas e o meio: estas, estando mais quentes, cedem energia ao ar circundante, para que se atinja o equilíbrio térmico.

O que se pode concluir quanto à emissão e absorção das latas? A lata pintada de preto, visto ser a que sofreu maior variação de temperatura durante o aquecimento, foi a que absorveu maior quantidade de energia. Tal facto deve-se à sua cor negra, que lhe garante um alto valor de emissividade.

A lata pintada de branco absorveu menor quantidade de energia, facto atestado pela sua variação de temperatura inferior durante o aquecimento, já que, visto estar revestida de branco, terá reflectido maior quantidade de radiação, tendo absorvido (e, consequentemente, emitido) menos energia. Assim, a emissividade da lata branca é menor do que a da lata preta.

A lata metálica foi aquela em que se verificou uma variação de temperatura durante o aquecimento menor, pelo que foi o corpo que absorveu menor quantidade de energia. Daqui se conclui que foi a lata com maior albedo e, consequentemente, maior emissividade.

A radiação incidente foi totalmente absorvida pelas latas? Não. As latas têm cores diferentes, pelo que absorvem e reflectem diferentes comprimentos de onda das radiações incidentes. A lata metálica, visto ter uma aparência espelhada, reflecte a maior parte da radiação que a atinge (maior albedo), pelo que é a que absorve menor quantidade de energia (menor emissividade), como se depreende pela sua baixíssima variação de temperatura durante o aquecimento; a lata branca reflecte grande parte da radiação incidente (a sua cor resulta da reflexão do azul, verde e vermelho, tal como se lê mais abaixo, nesta página), absorvendo uma quantidade reduzida desta, como se verifica pela sua baixa variação de temperatura durante o aquecimento; a lata preta absorve uma grande porção de energia incidente (maior emissividade), já que a sua temperatura varia, durante o aquecimento, muito, reflectindo uma percentagem reduzida (menor albedo).

Qual será a temperatura registada pelos sensores quando a temperatura das latas estabilizar? Durante o arrefecimento, as latas, visto estarem a uma temperatura superior à do meio ambiente, cederão energia aos corpos à sua volta. Assim, quando a temperatura destes recipientes estabilizar, ter-se-á atingido o equilíbrio térmico com o meio, sendo, por isso a sua temperatura igual à do exterior.

Era possível estudar o poder de emissão de superfícies diferentes, de acordo com o procedimento efectuado,  substituindo as várias latas pelo cubo de Leslie? O cubo de Leslie é um sólido metálico com algumas faces pintadas de cores diferentes. Assim, quando incide sobre uma delas radiação, este aquece. Embora a absorção esteja de acordo com as propriedades da cor da face, a emissão será feita através de todas as faces (que são superfícies diferentes) em simultâneo, pelo que não se pode estudar cada superfície individualmente. Por este motivo, o cubo de Leslie não poderia substituir as latas neste procedimento experimental.

 AL 10.1.2. Energia eléctrica fornecida por um painel fotovoltaico

   Durante a terceira actividade laboratorial, estudámos a potência fornecida por um painel fotovoltaico quando incidia sobre ele um raio de luz que podia variar em intensidade e no ângulo em relação ao painel. Sabendo que P=UI e que R=U/I (ver posts antigos nesta página), obtiveram-se os seguintes resultados:

   Daqui se conclui que há maior quantidade de energia fornecida ao circuito quando o raio incide perpendicularmente sobre o painel e a sua intensidade é máxima.

 AL 10.1.3. Capacidade térmica mássica

   Na quarta actividade laboratorial da unidade de Física, calculámos a capacidade térmica mássica de um corpo. Para tal, aplicámos a fórmula:

   A função f é a que traduz a temperatura (θ, em ºC) em função do tempo (t, em segundos): f(∆t)=∆θ. É o valor do seu declive (recorda que, em funções afim, como é o caso, g(x) = mx + b, sendo m o declive), obtido pela regressão linear na calculadora gráfica depois de se inserirem nesta os valores de temperatura (θ) medidos nos instantes (t) pedidos, que expressará o quociente entre variação de y ou f(x) (neste caso, a variação de temperatura, ∆θ) e a variação de x (neste caso, o intervalo de tempo, ∆t).

Porque é que no Verão a areia fica escaldante e a água do mar não? Uma vez que a capacidade térmica de um corpo é a quantidade de energia que é necessário fornecer-lhe para que a sua temperatura suba um grau Celsius (C = Q / ∆θ), para um mesmo valor de energia fornecida (Q), quanto maior for a variação de temperatura (∆θ), menor é a capacidade térmica (C) do corpo.
A areia e a água recebem a mesma quantidade de radiação, pelo que lhes é fornecida a mesma quantidade de energia (Q). Assim, o facto de a temperatura da areia variar mais do que a da água do mar (ficando a areia, por isso, "escaldante") permite-nos concluir que a capacidade térmica da primeira é menor do que a da segunda.

Porque é que os climas marítimos são mais amenos do que os continentais? Tal como em 1.1, tanto o solo continental como o oceano recebem a mesma quantidade de radiação e, por extensão, a mesma quantidade de energia. Contudo, verificamos que a variação de temperatura  do ar em contacto com o solo continental é superior à do ar em contacto com a água do mar (por isso o clima continental, o interior, é caracterizado por grandes amplitudes térmicas e o marítimo é mais ameno). Visto o ar possuir aproximadamente o mesmo valor de capacidade térmica independentemente da sua posição geográfica (conquanto que a altitude seja constante), pode concluir-se que o solo transfere maior quantidade de energia para o ar do que o oceano para que se atinja o equilíbrio térmico, logo o primeiro sofre maior variação de temperatura quando incide sobre ele radiação solar do que o segundo. Daqui se deduz que o oceano tem maior capacidade térmica do que o solo continental.

Suponha que tem duas cafeteiras de igual massa, sendo uma de alumínio (c = 900 J Kg^-1 ºC_-1) e outra de latão (c = 370 J Kg^-1 ºC_-1). As duas cafeteiras contêm massas de água iguais e são aquecidas, durante o mesmo intervalo de tempo, no mesmo disco do fogão. Em qual das cafeteiras a água atinge uma temperatura mais elevada? Justifique. Uma vez que a capacidade térmica mássica é a quantidade de energia que é preciso fornecer a um corpo, por quilograma de massa corporal, para que a sua temperatura suba um grau Celsius (c = Q / (m*∆θ)), para um mesmo valor de calor fornecido (Q) e uma mesma massa (m), quanto maior for a capacidade térmica mássica (c), menor será a variação de temperatura (∆θ) sofrida pelo corpo. Ambas as cafeteiras têm a mesma massa e contêm a mesma massa de água e a energia que é, para elas, transferida, visto a potência do disco de fogão e o intervalo de funcionamento deste os mesmos para ambos os casos, também é igual. Contudo, uma vez que a capacidade térmica mássica do alumínio é maior do que a do latão, este material vai sofrer uma variação de temperatura menor durante o aquecimento, transferindo, por isso, para a água, menor quantidade de calor do que o latão. Assim, a água da chaleira de latão atingirá maior valor de temperatura do que a na chaleira de alumínio.

 AL 10.1.4. Balanço energético num sistema termodinâmico

   Durante a quinta actividade laboratorial da unidade de Física, adicionou-se, a uma massa de água, água a 0ºC e, a outra igual, gelo a 0ºC para averiguar qual o método mais eficaz de arrefecimento. Sabendo que L_f é a quantidade de energia, por quilograma, de que uma substância necessita para que passe do estado sólido aos estado líquido, temos:

   A partir das fórmulas, compreendemos que é mais eficaz adicionar gelo, já que a quantidade de energia que este absorve até se atingir o equilíbrio térmico é maior (pelo que a temperatura final será inferior).

   Em ambos os procedimentos, a mistura deve ser agitada para que se uniformize a temperatura. No segundo caso, as pedras de gelo devem ser manuseadas rapidamente para que não se verifique troca de grande quantidade de energia com o meio e enxaguadas para que se adicione, à massa de água, apenas gelo e não uma mistura de água a 0ºC e gelo.

 AL 10.2.1. Energia cinética ao longo de um plano inclinado

 AL 10.2.2. Coeficiente de restituição

   O coeficiente de restituição de uma bola é dado pela raiz quadrada do declive da recta que assume a expressão Δh_ressalto = f (Δh_queda), que calculámos na aula. Esta grandeza está relacionada com a elasticidade do material, pois, quanto mais elástico for, maior será o seu coeficiente de restituição.

   Na aula, medimos, com um sensor CBR ligado à calculadora gráfico, as alturas de queda e ressalto de uma bola de voleibol, de modo a determinar-se o seu coeficiente de restituição.

Poder-se-á aplicar a Lei da Conservação da Energia Mecânica no estudo do coeficiente de restituição das diferentes bolas? Se considerarmos os instantes colisão com o solo (essenciais para determinar o coeficiente de restituição do corpo), visto a bola não ter regressado à altura donde foi largada após o embate, concluímos que houve dissipação de energia nesta interacção, pelo que não houve conservação de energia mecânica.

Qual das bolas tem maior elasticidade? A de basquetebol, visto ser a que possui o maior coeficiente de restituição, ou seja, aquela cuja altura no ressalto está mais próxima da altura de queda.

Em qual das bolas há maior dissipação de energia na colisão com o solo? A de voleibol, visto ser a que atinge a menor altura no ressalto face à altura de queda, isto é, a que possui o coeficiente de restituição mais baixo.

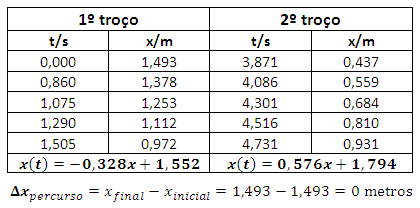
 AL 11.1.0. Corpos em movimentos a uma dimensão

   Um carrinho foi apetrechado com elásticos e colocado sobre uma calha de ar (de modo a minimizar a força de atrito). Após ser-lhe aplicada uma força, percorreu toda a distância da calha e, ao embater no final desta, regressou ao ponto de partida, repetindo estes movimentos várias vezes. Considerando apenas os primeiros dois trajectos, ou troços, foram tabelados cinco pontos de cada um destes para que se obtivessem as equações do movimento em ambos.

Qual é a origem do referencial adoptado? O sensor, pois a posição do carrinho é dada pela sua distância em relação a este aparelho.

Descreva o movimento do carrinho nos dois troços do referencial. O carrinho parte do final da calha e aproxima-se do sensor (desloca-se no sentido negativo da trajectória), percorrendo, com uma velocidade aproximadamente constante (a força resultante que actua sobre o corpo é aproximadamente nula), 1,493m em 3,011s. Nesse instante, o elástico do bólide embate no final da calha e o sentido do movimento é invertido (o vector deslocamento torna-se positivo), sendo que o carro regressa à posição inicial (x = 1,493m) 6,022s após o início da contagem dos tempos.

A variação de posição do carrinho ao longo do tempo será dado por uma expressão do tipo x (t) = mt + b (SI). O que são m e b? A letra m representa o declive da recta da função, que, como estudado nas aulas teóricas (ver gráficos posição-tempo), indica a velocidade do carrinho ao longo do movimento, em m/s. A letra b corresponde à posição inicial, em metros, do corpo em relação ao referencial estudado.

A velocidade escalar é constante ao longo de todo o percurso? Embora a velocidade ao longo de cada troço, esta é diferente para cada um deles (v₁ = 0,328 m/s e v₂ = 0,576 m/s) varia no momento de colisão com o final da calha. Assim, ao longo do percurso, esta não é constante: o movimento é rectilíneo e variado (note-se que «variado» não significa o mesmo que «uniformemente variado», pois o segundo tipo de movimento implica um valor constante de aceleração).

A que corresponde a área do gráfico velocidade-tempo de um dos troços? Esta área é igual ao deslocamento do corpo no troço.

Houve conservação de energia mecânica do sistema? Quando a energia mecânica é conservada, a soma das energias potencial gravítica e cinética é nula. Neste caso, como E_p=0 (não há deslocamento em altitude), ΔE_m=ΔE_c. Visto que a velocidade do carrinho não se manteve constante ao longo do percurso, houve variação de energia cinética no sistema, não se verificando, pois, conservação de E_m.

 AL 11.1.1. Queda livre

   A segunda actividade experimental do 11º ano consistiu na medição da aceleração adquirida por várias bolas quando largadas em direcção à Terra, de modo a determinar se o seu deslocamento poderia ser considerado o de queda livre. 

   Queda livre é o nome dado ao movimento de um corpo sobre o qual actua, somente, a força gravítica, F_g (desprezam-se outras forças, como a resistência do ar). Quando esta ocorre à face da Terra, temos:

Poder-se-á aplicar a Lei da Conservação da Energia Mecânica no estudo da queda das diferentes bolas? O estudo da queda das diferentes bolas, não considerando a colisão com o solo, indica-nos a intensidade da aceleração por elas adquiridas quando caem em direcção à Terra. Por comparação com o valor teórico que esta deve tomar, g (9,8 m/s²), todos os grupos (suponhamos que este foi, de facto, o caso) chegaram à conclusão que, visto o erro relativo ser aceitável (inferior a 10%), a queda dos corpos era livre. Assim, a única força a actuar sobre eles era a força gravítica, o que, visto esta ser conservativa, nos permite considerar que houve conservação de energia mecânica.

Classifica o movimento das bolas. É rectilíneo (pois as bolas são largadas verticalmente, numa trajectória em linha recta até ao solo) e uniformemente acelerado (visto a aceleração medida ser não-nula e constante).

Apresente três razões pelas quais a aceleração medida foi diferente de g. Durante o procedimento experimental, as bolas não foram largadas desprovido de ar, pelo que a sua resistência deverá ter causado uma variação na aceleração adquirida pelas bolas (note-se, que, ao haver resistência do ar, a força resultante a actuar no corpo não seria apenas a força gravítica, pelo que a aceleração por este adquirida não seria igual a g). Por outro lado, podem ter ocorrido erros durante a execução da experiência (a bola poderá ter sido lançada em direcção ao solo, em vez de largada, não sendo o seu movimento uma queda livre) ou erros do sensor na medição das distâncias e intervalos de tempo (a bola pode ter-se deslocado para fora da acção do aparelho, por exemplo).

Suponha que se realiza um ensaio com uma bola de praia grande e muito leve nas mesmas condições que neste procedimento experimental. Compare a aceleração desta bola durante a queda com g. A aceleração adquirida por este corpo seria bastante inferior a g, pois, uma vez que o corpo é muito leve e possui uma grande área de contacto com o ar, a intensidade da resistência deste gás seria muito elevada: F_r = F_g - R_ar <=> a = (F_g - R_ar) / m, logo, quanto maior for R_ar, menor será a aceleração da bola.

Dois atletas com massas diferentes em queda livre experimentam a mesma aceleração? Sim, porque, nesta situação, a sua aceleração é igual a g, valor que não depende das massas dos corpos (ver figura).

 AL 11.1.2. Movimento de um corpo com e sem força resultante nula

   Unindo dois corpos com um fio e recorrendo a uma calha e roldana, procurou-se, na aula prática de Física, responder à questão: «será necessária uma força para que um corpo se mova?». Os esquemas dos vários momentos do procedimento experimental assemelhavam-se aos da imagem abaixo.

Descreva o movimento do carrinho. Durante o intervalo de contagem dos tempos, o carrinho deslocou-se em linha recta ao longo da calha, no sentido positivo da trajectória. Entre os instantes x e y (enquanto a massa se manteve em queda), o gráfico v = v (t) assumiu a forma de uma recta de declive não-nulo, pelo que o corpo possuía aceleração constante (movimento rectílineo uniformemente acelerado). A partir deste ponto e até ao instante z (desde que a massa tocou no chão até que o carrinho foi parado e a contagem dos tempos terminou), a função e, consequentemente, a velocidade do carrinho foi, aproximadamente, constante, podendo dizer-se que o seu movimento foi rectilíneo e, aproximadamente, uniforme.

Para observar o movimento descrito pelo gráfico, que condições têm que ser asseguradas pelo grupo de trabalho? A calha onde se desloca o carrinho deverá ser rectílinea e estar colocada perpendicularmente ao raio da Terra (isto é, horizontalmente), o fio, inextensível, que liga os dois corpos terá que possuir comprimento que garanta que, quando a massa m toca no chão, o carro continua em movimento e o atrito deve ser minimizado (a bandeirola do carro pode ser encurtada, devem ser escolhidos materiais para a calha e para as rodas do veículo que, em conjunto, possuem um baixo coeficiente de atrito, etc.).

Que forma assumirá o gráfico posição-tempo deste deslocamento? Numa primeira fase, o carrinho desloca-se no sentido positivo da trajectória com movimento rectilíneo uniformemente acelerado, pelo que o x = x (t) será um ramo de parábola cuja concavidade está voltada para cima. A patir do momento em que a massa m toca no chão, a função torna-se uma recta de declive igual ao da tangente ao último ponto da parábola anterior, visto que o movimento do veículo se torna, sem haver inversão do sentido, uniforme (isto é, com aceleração nula).

Descreva o gráfico que expressa a evolução da energia cinética do carrinho em função do tempo, desde o início da contagem dos tempos até que a massa m toca no chão. A expressão, como se verifica abaixo, será do tipo y = ax², com a > 0, pelo que o gráfico que representa a função será o ramo de uma parábola cuja concavidade está voltada para cima.

Será necessária uma força para que um corpo se mova? Quando o carrinho estava parado, foi necessária uma força para que este se deslocasse; porém, após adquirir velocidade, manteve-a, mesmo depois da força resultante que sobre ele actuava se anular. Assim, concluímos que, para que um corpo se mova, só é necessário aplicar-lhe uma força quando este está em repouso. De acordo com a 1ª Lei de Newton:

 AL 11.1.3. Lançamento horizontal sem forças dissipativas

   Largando uma esfera de vários pontos com diferentes alturas (medidas com uma fita métrica ou régua) de uma calha inclinada assente sobre uma mesa que distava H = (904,5±0,5) mm do chão, calculou-se a velocidade que esta adquiria antes de ser projectada com base nos dados fornecido por um digitímetro ligado a uma célula fotoeléctrica e na medição, com uma craveira, do seu diâmetro ((13,12±0,01) mm). O alcance do corpo, isto é, o deslocamento horizontal deste entre a saída da calha e o embate no chão foi medido, para cada ensaio, com uma régua, sendo o ponto de colisão assinalado no papel de cenário que cobria o chão pela pressão exercida pela esfera no papel químico que se sobrepunha a esse.

   No estudo do lançamento horizontal da esfera, assumiu-se que o referencial tinha origem à saída da calha, ocorrendo o deslocamento da esfera no sentido positivo de 0x e no sentido negativo de 0y. Assim, o movimento horizontal da esfera após lançamento seria dado por x(t) = v₀t e o vertical por y(t) = (-1/2)gt² + H = -4,89t² + 0,9045 (SI).

Cálculo do tempo de queda experimental. A regressão linear da que melhor se ajusta ao conjunto de pontos que relaciona o alcance (variável independente, y) em função da velocidade à saída na calha (variável dependente, x) na calculadora é y = 0,3287x - 0,0164, logo temos x_máx = f(v₀) ⇔ x = 0,3287v₀ - 0,0164, em que x_máx é o alcance do corpo, em metros, v₀ é a velocidade inicial do movimento da esfera segundo o eixo 0x (velocidade à saída da calha), em m/s, o declive (m_f(v0) = 0,3287) é o seu tempo de queda ou voo, em segundos, e -0,0164 é o alcance, em metros, quando o módulo da velocidade à saída da calha é nulo.

Cálculo do tempo de queda teórico. Visto que os movimentos horizontal e vertical são independentes um do outro e que, durante o movimento, a esfera está sujeita à acção da força gravítica, podemos calcular o seu tempo de queda a partir da expressão que traduz o seu deslocamento em 0y.

Uma esfera é largada sem velocidade inicial (v_i = 0) numa rampa de altura h+H, em que H é a altura da mesa sobre a qual assenta em relação ao solo, ao longo da qual o atrito é desprezável. Qual a expressão que permite calcular o alcance da bola? Este dependerá da sua massa? Uma vez que o atrito é desprezável, ao longo do seu trajecto, a esfera conserva a sua energia mecânica, ou seja, ΔE_m = 0. Sejam E_mi e E_mf as energias mecânicas do corpo no ponto de largada e à saída da calha, respectivamente, e v₀ a sua velocidade à saída da calha. O alcance será dado por 2*√(Hh), pelo que não estará dependente da massa do corpo que se move.

 AL 11.2.1. Osciloscópio

   Na aula prática, foram estudados sinais eléctricos recorrendo-se a um osciloscópio, aparelho que mede a variação da diferença de potencial (eixo 0y é a tensão) de um gerador ao longo do tempo (eixo 0x é o tempo). Para além do convencional gerador eléctrico de corrente alternada (o osciloscópio mostrava uma linha horizontal com ordenada igual à tensão fornecida pela fonte) e contínua (o osciloscópio mostrava um sinal sinusoidal cuja diferença de potencial máxima (tensão de pico) era inferior à fornecida pela gerador (tensão eficaz)), ligou-se, ao osciloscópio, um gerador de sinais triangulares e quadrados e, depois, um microfone.
    Para a corrente alternada, verificou-se que Upico/Ueficaz = √2.

Para se medir uma tensão, a ligação entre a fonte de tensão e o osciloscópio tem de ser feita em paralelo. Porquê? O osciloscópio é um aparelho que mede diferenças de potencial e, por este, motivo, funciona como um voltímetro, necessitando, por isso, de ser ligado em paralelo ao gerador do circuito.

 AL 11.2.2. Velocidade do som no ar

   Com um bloco de madeira e um pedaço de metal (?), emitiu-se um sinal sonoro que seria recebido, primeiro por um microfone a 0 m do emissor e depois, por outro, a (6,790±0,005) m, de acordo com a leitura da fita métrica, do primeiro. Usando o programa Audacity num computador da escola, ligado aos microfones, foi possível determinar o intervalo de tempo entre a recepção do sinal pelo mais afastado e pelo mais próximo da tábua de madeira e, a partir desses dados, calcular a velocidade do som no ar. O valor teórico desta foi determinado com base na temperatura ambiente, medida com um termómetro.

Como se explicam as diferenças entre os valores teórico e experimental da velocidade de propagação do som no ar? A medição do intervalo de tempo entre a recepção do sinal acústico pelos dois microfones foi afectada pelos erros inerentes ao uso destes aparelhos e do software Audacity, podendo o grupo de trabalho, visto surgirem representadas, nesse programa, diversas ondas sonoras não associadas ao procedimento experimental, ter interpretado algum dos valores incorrectamente. A variação da densidade do ar, meio propagante, por movimentação das partículas pode, também, ter causado um decréscimo ou aumento da velocidade do som durante a experiência, sendo, em conjunto com o erro associado à medição de temperatura com um termómetro, que influenciará o valor teórico de v, um factor que justifica as diferenças entre os valores experimental e teórico calculados.

Como estudar a variação da velocidade do som no ar em função da temperatura? Através da repetição do procedimento experimental descrito neste protocolo — medição do intervalo de tempo entre a recepção de um sinal acústico por dois microfones sendo a distância entre estes fixa e conhecida — em situações com condições de temperatura diferentes mas bem definidas, isto é, determinadas com o auxílio de um termómetro, por exemplo.

Dois amigos pretendem medir o comprimento de um túnel emitindo em simultâneo um som intenso e um sinal laser numa das suas extremidades e calculando o intervalo de chegada dos dois sinais ao fim do túnel. Avalie este método. Assumindo que o túnel mencionado se trata de um rectilíneo (se tal não for o caso de tamanho da ordem das centenas de metros imerso num meio material de propriedades conhecidas (ar, por exemplo), o sinal luminoso atravessá-lo-á quase instantaneamente, pelo que o intervalo de tempo medido será, na verdade, o tempo de percurso do som pelo túnel [unfinished].

Anexo A: Noções básicas de circuitos eléctricos

   A tensão (U, expressa em volts, V) ou diferença de potencial é a energia que o gerador fornece ao circuito, por unidade de carga que o atravessa. Pode ser medida com um voltímetro, que deve ser ligado em paralelo.

   A intensidade (I, expressa em amperes, A) é a quantidade de cargas eléctricas que atravessa o circuito por unidade de tempo. Pode ser medida por um amperímetro, que deve ser ligado em série.

   Numa associação em série, a intensidade da corrente é sempre igual em qualquer ponto do circuito. A tensão aos terminais da pilha é igual à adição da tensão medida aos terminais da lâmpada 1 e a tensão medida aos terminais da lâmpada 2.

   Numa associação em paralelo, sucede o contrário: a intensidade da corrente aos terminais da pilha é igual à soma da tensão aos terminais da lâmpada 1 com a tensão aos terminais da lâmpada 2, mas a tensão é sempre igual em qualquer ponto do circuito.

   A resistência eléctrica (R, expressa em ohms, Ω) de um condutor eléctrico traduz a oposição deste à passagem da corrente eléctrica e pode ser medida por um ohmímetro. Em condutores óhmicos, aplica-se a Lei de Ohm: R=U/I.


-----------------------------------------------------------------------------------------------

ⁱÉ por este motivo que, citando a 2º Lei da Termodinâmica, num sistema isolado, a quantidade de energia útil nunca aumenta. ↑

ⁱⁱLei da Conservação da Energia: Num sistema isolado, a quantidade total de energia permanece constante. ↑

ⁱⁱⁱPor convenção, a energia cedida por um sistema é representada por um valor negativo (por exemplo, -256 J) e a que é recebida por este é representada por um valor positivo (por exemplo, 768 J). A expressão aqui exposta que traduz a 1ª Lei da Termodinâmica obedece a este princípio. ↑

^ivO equilíbrio térmico consiste numa igualdade entre as temperaturas de dois corpos em contacto e implica que cada um deles ceda a mesma quantidade de energia que recebe. De acordo com a Lei Zero da Termodinâmica: Dois sistemas em equilíbrio térmico com um terceiro estão em equilíbrio térmico entre si. ↑

^vA um líquido ou gás pode dar-se o nome de fluido. ↑

^viNum colector solar plano, existe um vidro ou plástico na face superior de uma caixa cujas faces (com excepção da superior) são constituídas por materiais isolantes. No fundo da caixa há uma placa absorsora, pintado de preto baço, sobre a qual existem tubos absorvedores (geralmente de cobre) nos quais circula o fluido de transferência. A luz, ao incidir sobre o colector, atravessa a sua tampa de vidro ou plástico (que contribui para um efeito de estufa, já que é transparente à radiação visível do Sol mas não à IV, emitida pelos componentes do objecto, reenviando-a para o interior da caixa) e fornece energia aos tubos absorvedores, que a conduz (estes são, geralmente, feitos de cobre, porque, devido à sua condutividade térmica elevada, conseguem conduzir o calor rapidamente) para toda a sua extensão e para o fluido de transferência. Ao ser aquecido, este realiza movimentos de convecção, sendo que a sua porção mais quente sobe (convecção natural) ou é bombeada (convecção forçada), no interior dos tubos, para um depósito de água. Aí, a energia transfere-se do fluido para os tubos e destes para a água, aquecendo-a. A cedência de energia arrefece o fluido, que então desce (convecção natural) ou é bombeado (convecção forçada), através dos tubos, de volta ao colector. ↑

^viiNa aula, não usámos o termo «variação de entalpia», mas utilizámos, em diversos cálculos um valor de energia designado L_f, que não é mais do que a ΔH necessária para causar a fusão de uma substância. Ver Balanço energético num sistema termodinâmico para informações sobre a aplicação destas grandezas no cálculo da energia recebida por um corpo. ↑

^viiiVer páginas 164 e 165 para explicações sobre a adição de vectores. ↑

^ixVer Energia cinética ao longo de um plano inclinado para a aplicação desta lei. ↑

^xA 2ª Lei de Newton diz-nos que um corpo de massa m, sujeito a uma força resultante F, adquire uma aceleração a que tem a mesma direcção que a força e uma intensidade que é directamente proporcional à força e inversamente proporcional à massa, isto é, F_r = m * a. ↑

^xiA aceleração gravítica é uma constante que depende do local onde é medida. Na Terra, este valor é cerca de 9,8 N kg^-1 ou 9,8 m s^-1 (as unidades são equivalentes). ↑

^xiiLei da Conservação da Energia Mecânica: Quando, sobre um sistema, só actuam forças conservativas, a sua energia mecânica mantém-se constante. ↑

^xiiiOs conceitos repouso e movimento são relativos: por exemplo, um passageiro imóvel num comboio a viajar a 120 km/h está em movimento em relação à linha férrea, mas em repouso em relação ao próprio comboio. ↑

^xivQuando este é cartesiano, as letras que designam os eixos devem ser sequenciais (ordem alfabética) e estar dispostos no sentido anti-horário. (exemplo) ↑

^xvA velocidade média é uma grandeza física de carácter vectorial que resulta da divisão do deslocamento de um corpo (um vector, como estudado no 10º ano no contexto do cálculo do trabalho das forças, com origem na posição inicial do corpo e extremidade na sua posição final que indica a variação de posição de um corpo e que, por isso, aponta também o sentido e a direcção do movimento) pelo intervalo de tempo em estudo.A aceleração média também é uma grandeza física de carácter vectorial. Para simplificar a abordagem destes conceitos, o programa do 11º ano de Física exige apenas o cálculo da velocidade média escalar, cujo sinal (negativo ou positivo) indica o sentido do movimento, e da aceleração média escalar. ↑

^xviVer figura 35 da página 29 do manual. ↑

^xviiUm corpo negro é um absorsor perfeito, porque absorve toda a radiação que sobre ele incide (α = 1), sem transmitir (ι = 0) ou reflectir (ρ = 0) qualquer fracção dela. Assim, como ε = α, emite toda a energia que recebe (emissor perfeito, ε = 1). ↑

^xviiiA radiação solar directa é aquela que incide perpendicularmente à superfície da Terra. Devido à sua esfericidade, a superfície terrestre não recebe igual valor de intensidade. Sendo esta grandeza traduzida pela potência por unidade de área, à medida que aumenta a inclinação dos raios solares, mantém-se o valor da potência e aumenta a área da superfície, pelo que diminui a intensidade recebida. ↑

^xixO efeito de estufa é provocado pela existência, nas camadas mais baixas da atmosfera, de GEE (gases com efeito de estufa), como dióxido de carbono, ozono troposférico (também apelidado de "ozono mau" por ser tóxico para os seres vivos), óxidos de azoto e metano. Estas moléculas são transparentes às radiações de pequeno comprimento de onda provenientes do Sol que atingem estas altitudes baixas (transmitem-nas, isto é, deixam-se atravessar por elas), mas absorvem os seus raios infravermelhos e os da Terra. Esta energia é, depois, emitida em todas as direcções, sendo que parte é reenviada para a superfície terrestre, impedindo a diminuição da temperatura junto a ela, isto é, mantendo uma temperatura amena e propícia ao desenvolvimento da Vida e assegurando uma baixa amplitude térmica. O aumento da concentração destes gases na atmosfera, significa, contudo, que a energia solar ficará "aprisionada" durante um maior intervalo de tempo junto ao solo. Assim, a potência recebida pelo planeta será superior à emitida por este (= desequilíbrio radiativo), ou seja, acumular-se-á, na Terra, energia, o que causará um aumento da sua temperatura média (= aquecimento global). Assistiremos, pois, ao degelo das calotes polares e dos glaciares e a um período de acentuadas alterações climáticas que poderão levar a uma extinção em massa. ↑